Chapter 3 What is Computational Neuroscience?

3.1 Vocabulary

• Algorithm
• Bottom-up processing
• Computational neuroscience
• Computational theory
• Decoding model
• Emergent phenomena
• Hardware and implementation
• Model
• Neural decoding
• Reconstruction
• Reductionism
• Representational model
• Top-down processing
• Turing Machine
• Turing-complete
• Turing test

3.2 Introduction

Look at this picture of a desk on the page in front of you. Your brain is somehow able to translate the raw sensory data coming from your eyes into a judgment about the identity of the object in the image. If we want to build a machine that can demonstrate a similar capacity to judge, then we need to be able to model and understand the mechanisms that are at work when we see the image. This leaves us with at least two questions:

• How might we create a computer program that performs the same cognitive tasks as us humans?
  
• What can such a program tell us about the mechanisms at work in our own human brains?

While these questions may not be exhaustive of all the concerns of computational neuroscience, they should at least give you a taste of some of the issues the discipline grapples with on a regular basis.

3.3 What is computational neuroscience?

Computational neuroscience is an interdisciplinary field that applies the principles of mathematics, philosophy, and computer science to study the inner workings of the brain. Computer models are critical to computational neuroscience, because they allow experiments to be conducted in a highly controlled and replicable fashion. In this context, a model is a simplified version of a system that tries to simulate how that system would behave in the real world.

For example, suppose a computational neuroscientist wants to understand how the human brain begins to make sense of sounds. They would construct a computer model for this purpose as already many aspects of the hearing parts of the brain have been measured and are ready to use. Such measurements would make constructing a useful computer model possible since they would constrain the design model. In other words, our researcher could design a model where the simulated features match the measurements of the corresponding real features of the brain. This model could be useful because our researcher has access to all the features of the computer model—including those that could not be easily and ethically measured in the actual human brain. This utility would be born out in plausible inferences about currently unmeasured properties and behaviors of the brain.

Like any other scientific field, inferences can be dynamic as developments are emerging rapidly. New research and new technologies are always pushing the boundaries forward. Being a developing field, even if a model brings us no complete certainty, it can also be worthy in shaping approaches to problems and also help with scientists developing artificial intelligence.

3.3.1 Can we make models that understand?

Considering the potential computer models of the brain, it may be tempting to think you could build a model that truly “understands” in the same way that a human person does. It seems exciting, think of the possibilities. We could then conduct intricate experiments that we could not perform on human brains. Perhaps we could create sentience? But maybe that might be a confusing way to start since commonly we think that computers are not much more than the devices we commonly use. However, computation in terms of understanding computational neuroscience is more diverse and can be more theoretical than simply typing commands in our laptops. Computation, a very vast field, includes mathematical steps, processes and interpretations which could or could not be calculated with a physical computer machine. It is this definition that leads us to think more broadly about computational neuroscience and what it means to discover, whether we create a brain inside a physical computer or even theoretical machines. “Understanding” as such is one important aspect but what if even when we create a human brain in a computer, that could understand, would we still be able to know how our brains work? What would it mean then for a computer model to “understand”?

Most notably, Alan Turing started the discussion. He created the Turing Machine. It is a theoretical machine that can do any calculation. The machine has a finite number of configurations and an imaginary infinite tape that is read by the machine. The purpose is to solve issues in an “effective procedure”, which means to solve a problem in an effective way, it is mechanical and needs to finish the problem in a finite number of steps Any problem that can be solved using a Turing Machine is computable. Many items that can solve computational problems are equivalent to Turing machines, and these are called Turing-complete. Computation’s scope goes beyond the physical computer that we are used to.

This machine paved the way for the Turing Test, where a machine that develops language interacts with a person via text and the person has to decide if their correspondent is human or not. If so, we could say that the machine has reached human intelligence. Given the complexity of the topic, it is appropriate to say that establishing when artificial intelligence will be comparable to human intelligence is an ongoing problem today.

On the side arguing that a computer model could never truly understand something the way a human does is philosopher John Searle. Searle makes use of his famous “Chinese Room Argument” to suggest that merely following a set of rules to produce a desired result from a given input is not enough to count as true understanding. For example, Searle would argue that using a big book of rules for writing answers in Chinese characters that respond to Chinese questions is not the same thing as having a natural conversation in Chinese—you are performing the function but there is no understanding. ¹. The system could fake being intelligent and ‘understanding’ while actually being ignorant itself.

This may seem intuitively true, but many of Searle’s opponents ² argue that Searle’s argument is only intuitively true. That is to say, Searle is merely provoking intuitions rather than supplying premises or facts that lead to his desired conclusion. Still taking on Searle, we can consider that while the person themselves does not understand Chinese, the system as a whole does. So even though the model could not understand like a human, the aggregate processes could, and functionally that would be the case. This can help us think in computational neuroscience about the different ways we consider the outcomes of research and what computing through our goals would actually look like.

In the link below, you can play Conway’s Game of Life. It is a Turing-complete program, that follows all the rules of the machine, it is unending, and has interesting limitations to imitate and calculate life. It is a zero-player game that only starts with the initial configuration and checks itself, just like a Turing Machine, and adjusts as the game goes on until certain conditions have been met.

Figure 3.1: Example of Conway’s Game of Life

3.4 Levels of organization

In 1982, David Marr introduced a new approach to analysis. He believed that there were three levels of analysis when considering the model of the brain.

• The computational, deals with the problem solving aspect: why we need this model and what it explains. This approach is geared towards problem solving and the logic of our model.

For example, if we are given two boxes, each with a different number of books, and we need to know the total number in both, we know we have to use addition as a strategy. The input is two numbers, and the desired output is the sum of those numbers.

• The second level consists of the representational scheme and the algorithm, it is the how part. The representational scheme is the way in which we represent the input and the output in whatever system we are implementing the algorithm. The algorithmic is the set of operations that are performed with or by those elements in order to carry out the transformation specified by the computational theory.

One example is a cookbook recipe; this will define a step by step process (i.e., an algorithm) for how to produce a product given a set of clearly defined ingredients (i.e., a representational scheme).

• The third level is hardware implementation, which refers to the physical machinery that realizes the algorithm and the representation in a physical way.

For example, if you try to withdraw money from an ATM, the machine will run the algorithm designed for the purpose. The hardware implementation part comes in when the machine brings the money in the cash dispenser for you to grab.

The goal of computational neuroscience is to be able to model and replicate the functions of the brain in a non-organic setting. One of the ways to do this is through computer programming software, such as the application Python.

Consider the following basic code:

Here is an example of an arithmetic addition problem coded in Python. We can see the input, the algorithm which is transforming the input, and then the correct output of 4. Given the properties of coding software such as Python, which takes input, and runs it through a set algorithm, is this similar to the way we humans do it? If so, how? If not, why not?

3.5 Applications of computational neuroscience

As we delve deeper into computational neuroscience, we find that the field has a variety of potential applications when it comes to understanding cognition. Perhaps most distinguished is computational neuroscience’s ability to create models of our cognitive processes, such that they are able to capture the basis of complex phenomena through mathematical models and computer simulations. The brain is an extremely complex organ, and while we may not always understand all its structures and functionality, by using various methods of computational neuroscience, we can abstract certain understandings and model them. In doing so, we develop the ability to understand interactions between neurons in the brain and begin seeing the nature of certain causal and correlational relationships.

Furthermore, we can begin to predict how complex systems in the brain will behave when presented with particular stimuli. This may all seem rather abstract, so let’s think of an example we often take for granted: Vision. How is it that we are capable of recognizing a variety of highly specific things and can distinguish them from one another? What constitutes recognition and the neural processes behind it? How do we decide what registers as recognition and what doesn’t? Why is it so difficult to replicate these seemingly innate processes in a robot? We can approach these questions and attempt to address them using computational neuroscience. When we think of how to model vision, the first thought is to do it in the most simple manner possible. This makes sense. Whether or not we implement the “right” level of simplicity when creating models is difficult—if not impossible—to discern. It should be acknowledged that the desire to create computational models in the first place stems from our curiosity of understanding the brain. Therefore, we must be cognizant of this and engage any model that is created with criticism and scrutiny.

Figure 3.2: One example of emergent phenomena are the flight patterns of geese. One goose alone flies as it wishes but a collection of geese come together to form a v-shaped pattern that affects the overall movement of the geese.

You may be saying to yourself, “Ok, this is great in theory, but where do we begin?” Let’s start by thinking about the big picture. Think about the setup of a system. If we want to understand how it works, we first need to understand how it is organized. This is where a term called emergent phenomena comes into play. Emergent phenomenon is the cyclical dissemination of recurrent information from a micro to macro perspective and vice versa. It allows us to reframe composite systems such that we are able to understand their underlying mechanisms in simpler terms. For example, take our understanding of the brain. Known information about the brain alters following the release of new research, which changes depending on the trends in different interests in research. In turn, this changes the research being done, which then modifies our knowledge about the brain. This permits emergent phenomena to highlight both the mechanics and the nature of a particular system. Let’s look at another example.

What makes something a car? Well, it can be ascertained that most cars have four wheels; this is part of its mechanic. However, that is only one part of the whole. Four wheels do not constitute a car; what allows us to identify one is the essence of “car-ness” that is derived from the singular amalgamation of all its parts. These methods of thinking relate to two primary schools of thought: Reductionism and Reconstructionism. Reductionism is the idea that in order to understand a given complex system, we must be able to reduce it to its simplest form, while Reconstructionism asserts that understanding a system relies on the ability to reconstruct the system such that we are able to capture its complexity. Think of Reductionism and Constructionism in terms of the brain. Reductionism is akin to studying one neuron, or a group of neurons to derive its function, while Reductionism involves analyzing how the brain functions as one system. This matters because when we create models of the brain, it is not sufficient to only explain its architecture. We must also show how the architecture gives rise to certain relationships and interactions—but how?

Let’s look at how two different types of models approach this. One type of model, called the decoding model, helps us understand the brain’s computational mechanisms by unveiling the information present in various locations of the brain. The idea is that if brain activity is able to be decoded, then information is present. To clarify, Neural Decoding is the process of interpreting the information that resides within neuronal activity (i.e., action potentials). You will read more about this in Chapter 7. When that information is considered “representational” of that specific brain region—meaning it carries significance and pertains specifically to that location—we can subsequently analyze the purpose of this information as it is sent and received from different regions of the brain. This information allows us to better understand brain functions and how information is transmitted, which can then be implemented in computational models.

On the other hand, we could also use representational models. These types of models are more all-encompassing than decoding models; they specify what representation looks like within a brain region. Given an exhaustive list of random stimuli, we predict how that region of the brain would respond. Knowing all the possibilities of neuronal responses allows us to predict which stimuli can be decoded.

Representational models provide greater computational restraints about the predictions made in representational space than decoding models. While representational models do not provide us with a direct path to the creation of a computational model, the predictability of neuronal behavior within representational spaces can lead to the creation of computational models that can respond to novel stimuli. You may have also noticed that these two models themselves do not actually perform the functions or tasks that these computational models ask for. They do not happen to explain the mechanisms behind the tasks, but they provide constraints for the computational models. This is one of the first steps to approaching a fully integrated computational model.

Figure 3.3: This image can be approached in two different ways. For bottom-up processing, we can see the letters first and then figure out the words. For top-down processing, we can see the words and decide what each letter is.

As we can see, these are merely two types of models that vastly differ from one another. There are many more. How did they come to be? They may all be extraordinarily unique in their perspectives, but there is one commonality they all generally share. We design our models using one of two following approaches: Top-down processing or bottom-up processing. Top-down processing makes us design our models with a certain purpose, or goal in mind. Bottom-up processing leads us to establish a base of information or data before creating the model, and then creating the model and its purpose from what we have collected. As you process this information, think about how decoding models and representational models fit into these schemes.

3.6 The future of computational neuroscience

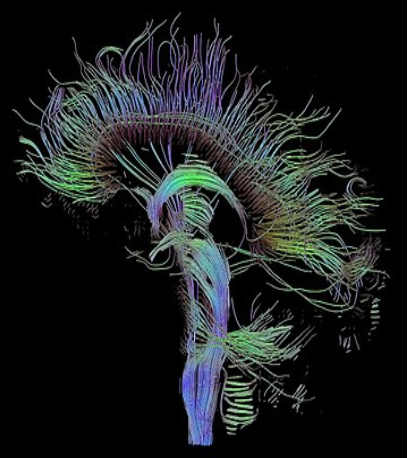
Figure 3.4: Hebbian learning is the strengthening of connections between postsynaptic and presynaptic neurons based on activity-dependent synaptic activity. Applying Hebbian theory to computational neuroscience allows us to envision the connections between various neurons in the brain, displayed here is what is called a ‘connectome’.

Given all this information, what is the future of computational neuroscience? Interest in the field is increasing steadily and every day the range of its possible applications grows. In 2013, the Obama administration began the BRAIN initiative, a program designed to facilitate the development of innovative technologies that allow for a well-rounded and versatile understanding of brain function. In 2005, a Swiss team of scientists began another initiative called the Blue Brain project whereby they reconstructed the mammalian brain using simulations to generate a comprehension of the basic underlying principles of brain function and architecture. Computational neuroscience becomes more relevant everyday. Not only does it allow us to tackle difficult issues like the complexities of Hebbian learning and Neural Networks, but it is relevant in everyday applications too. For instance, recent breakthroughs in robotic neuroprosthetic systems may lead to a future in which paralyzed individuals could control prosthetic limbs using tiny implants or wearing electrodes. All of this is due to our detailed understanding of the neural processes involved in motor control; recognizing these processes allows us to create algorithms that can replicate that stimulation. This is merely the beginning. Many fields, including computational neuroscience, are trying to develop our understanding of the brain and many more will.

3.7 Summary

Every person has a brain, but that does not mean we truly understand what the brain is (We should also think: What does it mean to understand the brain?>), or what it does. It is a complex organ with a multitude of facets to understand. To fully grapple with it, you must understand the mechanics and the reasoning behind each component. Computational thinking is one manner of striving towards this goal.

Computational neuroscience is a complex field that translates much of what we understand as biological constraints and cognitive processes and uses this to create a model of the brain, employing mathematical models and theoretical analysis to better understand the brain’s functions. The principles that govern computational neuroscience and its abstractions utilize several types of processes and manners of thinking. In this chapter, we examined what computation means, how Marr’s three levels of investigation provide structure for any information processing system; how models are created using top-down or bottom-up processing; how emergent phenomena organize a system; and how machines operate, thanks to Alan Turing. The integration of cognitive neuroscience along with the development of more complex technologies and Artificial Intelligence may be the future to understanding the brain one day. In an era of rapid scientific discoveries, progress is being made daily. Many have been striving to achieve this goal, and many more will continue to do so.

3.8 Exercises:

1. Consider at least two methods you could use to add two integers such as 5 and 5. Which of Marr’s levels changes as a result?
   
2. Explain the difference between the top-down and bottom-up philosophy.
   
3. Which better explains and represents cognitive phenomena: the top-down approach, or the bottom-up approach?
   
4. Characterize the concept of emergent phenomena. Does human sentience embody the phenomenon?
   
5. Does artificial intelligence have to contain emotions to be sentient?
   
6. Would we consider the brain a computer?

---

1. See https://plato.stanford.edu/entries/chinese-room/ for more on this thought experiment.↩︎

2. E.g. Dennett, Thagard, and Pinker to name a few↩︎